Laboratorio 6: Filtros de Agudizamiento o Sharpening

En el laboratorio anterior vimos los Filtros de Suavizamiento, ahora veremos los Filtros de Agudizamiento, cuya función en realzar los detalles finos de una imagen.

Estos filtros se basan en la primera y segunda derivada. Y así como los filtros antes vistos también es necesario el uso de una máscara o kernel, que será la que define los cambios que se producen en la imagen, en este caso dependerá de dicha mascará cuanto es el realce de los detalles.

Iniciaremos describiendo los Filtros Laplacianos.

FILTROS LAPLACIANOS
Se define con la siguiente fórmula: (1)

Donde se tiene la suma de las derivadas con respecto a x y con respecto a y. Definidas: (2)
Entonces reemplazando (2) en (1) tenemos la siguiente expresión:

que corresponde a los detalles de la imagen, ahora debemos agregar estos detalles en la imagen, pero puede ser que se sumen o se resten, finalmente con la siguiente expresión obtendremos la imagen con los detalles realzados:

Veamos un ejemplo, utilizando la siguiente imagen original:
Usando la máscara:
Obtendremos la siguiente imagen, donde se nota el realce de los detalles.

Ahora usando otra máscara:Obtenemos:

Si usamos una máscara diferente, por ejemplo la siguiente, que tiene un coeficiente central positivo:

Vemos que la imagen resultante es más clara que utilizando los dos filtros anteriores, sin embargo también se realzaron sus detalles.

UNSHARP MASKING AND HIGH-BOOST FILTERING

Este tipo de filtrado se usa cuando la imagen es muy oscura y necesitamos aclararla.

Consiste en obtener una imagen, a la cual se le resto su versión suavizada (es decir la imagen borrosa). Podemos obtener la imagen suavizada con la siguiente expresión: (1)

Ahora definimos al filtro high boost de la siguiente manera: (2)
Si reescribimos la ecuación, de acuerdo a la definición (1), obetendremos:
Donde:
fs: Imagen suavizada usando filtro laplaciano o cualquier filtro de suavizamiento.
A: Variable.

Si usamos un filtro lapaciano, obetendremos:
Ahora, con un ejemplo veremos los resultados obtenidos.
Imagen original:
Valor de A=2.
Si usamos un filtro de suavizamiento, por ejemplo el Filtro Promedio, obtenemos:
Pero si usamos un filtro lapaciano, con el mismo valor de A, notamos que aclaró más a la imagen:

DETECCIÓN DE BORDES:

Usando la definición de la primera derivada, logramos obtener los bordes en una imagen, veremos dos operadores, el de Roberts y el de Sobel, probaremos ambos casos con la siguiente imagen:

ROBERTS
Según Roberts, el cálculo de la primera derivada se hace de la siguiente manera:
Por ejemplo con una máscara de 3x3:

Si aplicamos esta definición a la imagen original anterior, obetenemos:


SOBEL
Ahora, tenemos una definición distinta de como encontrar la primera derivada, Sobel lo define de la siguiente manera:
Lo aplicamos a la imagen original y obtenemos:

Notamos que los bordes son más dominantes.

CASO DE ESTUDIO
Aplicando los fitros vistos: laplaciano, sobel, incluso los de suavizamiento, intentamos mejorar una imagen de scaneo de huesos, para detectar infecciones de huesos y tumores.
Tenemos la imagen original:

Seguimos los siguientes pasos:
1. Aplicamos filtro laplaciano y realzamos la imagen.
2. Aplicamos el operador Sobel.
3. Suavizamos la imagen de sobel con un filtro promedio.
4. Ahora obtenemos Laplaciano*Sobel Suavizada.
5. Sumamos: ImagenOriginal + Laplaciano*Sobel Suavizada.
6. Aplicamos operacion potencia al resultado anterior (y=0.5, c=1)
Finalmente obtenemos:

Donde se puede ver claramente la mejora, aunque también se tiene la dificultad de que la imagen contiene ruido.

Laboratorio 5: Filtros

Los filtros son técnicas que permiten atenuar o eliminar el ruido de las imagenes en esta oportunidad describiremos y ejemplificaremos los filtros de suavecimiento lineal y estadisticos

Para la prueba de los algoritmos utilizaremos la siguiente imagen con ruido

• Filtros de suavecimiento Lineales: Llamados filtros promedios, consiste simplemente en promediar los pixeles que caen dentro de la mascara, son llamados tambien filtros de paso bajo se usan para reduccion de ruido, y eleiminar detalles detalles irrelevantes Utilizando la siguiente mascara:

obtendremos el siguiente resultado:

Utilizando la siguiente mascara

Se obtiene el siguiente resultado

otro caso es utilizando una máscara como la que se muestra a continuación

Se obtiene el siguiente resultado

Utilizando un filtro gausiano con una mascara de convolucion de 3 x 3 se tiene

• Filtros de suavecimiento Estadisticos:
  

1. Filtro Max: Se considera el valor mas alto de los pixeles ordenados, este método busca puntos brillantes en la imagen.
   
   

2. Filtro Min: Se considera el valor mas pequeño de los pixeles ordenados, busca puntos oscuros en la imagen

3.Filtro del punto Medio: Escoger el valor máximo y mínimo dentro de la ventana y promediarlos
4. Filtro de la Media Geométrica: trabaja mejor con ruido gaussiano, se comporta mal con ruido tipo sal y pimienta, utiliza la siguiente formula:

Resultado obtenido:

Laboratorio 4: Casos de Estudio

caso 1 Promedio de una Imagen
Consideramos una imagen ruidosa g(x,y) formada por la adicion de ruido n(x,y)para una imagen original f(x,y); eso es representado por: Se asumira que en cada par de coordenadas(x,y) el ruido es no correlacionado y tiene un promedio cuyo valor es cero. El objetivo del siguiente procedimiento es reducir el contenidode ruido adicionando un conjunto de imagens ruidosas, formalmente representado por:

Utilizaremos las siguientes imagenes para probar este método sumaremos intercaladamente las siguientes imagenes 10 veces.

imagen 1

imagen 2

resultado del metodo explicado

Caso 2 Uso de las estadisticas del histograma para mejoramiento de imagenes

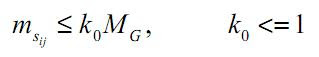Realizaremos la explicación de este proceso atraves de un caso de estudio que describiremos a continuacion: Mejoraremos el contraste de las areas oscuras pero sin alterar las áreas claras para ello utilizaremos un método local basado en las estadísticas de la imagen para ello compararemos la media local de una sub imagen con la media global representado por:para analisar el pixel p(i,j) es candidato para procesamiento, esto es una buena táctica para saber si una region es clara o oscura, comparamos la desciacion estandar local de una sub imagen con la desviacion estandar global para detrminar las areas que tienen bajo contraste

el valor de la constante sera mayor que uno si se quiere incrementar el contraste de áreas claras y menor que uno si se desea incrementar el contraste de las áreas oscuras
finalmente se tiene que realizar una restriccion mas, en areas que tiene valores iguales, es decir desviaciones estandares=0 (o cercanos a cero)

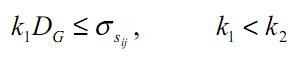los pixeles que pasan dicha condición se incrementan o decrementan su valor de intensidad multiplicandolo por una constante E, los demas se dejan sin procesar sumarizando se tiene

Para probar el método utilizaremos la siguiente imagen

Resultado obtenido